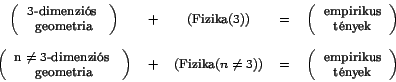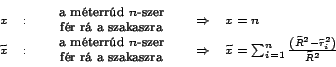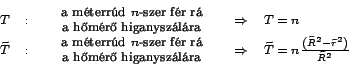6. A Poincaré-féle konvencionalizmus és a Duhem-Quine-tézis
Le lehet-e vezetni egy fizikai elméletből bármilyen, a téridő geometriájára,
és általában, szerkezetére vonatkozó állítást. Poincaré
úgy gondolta, hogy nem. A térre és időre vonatkozó állításaink konvencionálisak.
Képletesen szólva
Mi döntjük el, hogy hol választjuk szét a geometriát és a fizikát,
vagyis lehetséges több
Poincaré ezt a következő példán mutatta meg: Gondoljunk el kétdimenziós
lényeket, akik arra vannak kárhoztatva, hogy egy közönséges euklideszi
körlap belsején éljék életüket (![[*]](file:/usr/local/share/lib/latex2html/icons/crossref.gif) . ábra). Vannak
méterrúdjaik, melyekkel távolságot tudnak mérni. A körlap hőmérséklete
a középponttól kifelé haladva a
. ábra). Vannak
méterrúdjaik, melyekkel távolságot tudnak mérni. A körlap hőmérséklete
a középponttól kifelé haladva a
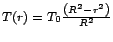 formula szerint csökken. Méterrúdjaik a hőmérséklettel arányosan változtatják
hosszukat, tehát a kör széléhez közelítve a méterrudak hossza nullához
tart. Poincaré megmutatta, hogy ha e körlap lakói úgy veszik, hogy
méterrúdjaik hossza mindenütt egyforma, akkor arra a konklúzióra jutnak,
hogy egy végtelen kiterjedésű, konstans negatív görbületű Bolyai-Lobacsevkszki-felületen
élnek. Vagyis megint a geometria és a fizikai elmélet együtt kell
hogy megfeleljen mindannak, amit e kétdimenziós lények műszereikkel
és érzékszerveikkel a világból tapasztalnak:
formula szerint csökken. Méterrúdjaik a hőmérséklettel arányosan változtatják
hosszukat, tehát a kör széléhez közelítve a méterrudak hossza nullához
tart. Poincaré megmutatta, hogy ha e körlap lakói úgy veszik, hogy
méterrúdjaik hossza mindenütt egyforma, akkor arra a konklúzióra jutnak,
hogy egy végtelen kiterjedésű, konstans negatív görbületű Bolyai-Lobacsevkszki-felületen
élnek. Vagyis megint a geometria és a fizikai elmélet együtt kell
hogy megfeleljen mindannak, amit e kétdimenziós lények műszereikkel
és érzékszerveikkel a világból tapasztalnak:
Figure:
Képzeljünk el olyan kétdimenziós lényeket, akik egész életüket
egy euklideszi körlap belsejében élik le. Vannak méterrúdjaik, melyekkel
távolságot tudnak mérni. A körlap hőmérsékleteloszlása nem homogén.
A középponttól kifelé haladva a
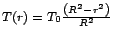 formula szerint csökken. Tegyük fel az egyszerűség kedvéért, hogy
méterrúdjaik a hőmérséklettel arányosan változtatják hosszukat, tehát
a kör széléhez közelítve a méterrudak hossza nullához tart. Könnyen
belátható, hogy ha e körlap lakói úgy veszik, hogy méterrúdjaik hossza
mindenütt egyforma, akkor arra a konklúzióra jutnak, hogy egy végtelen
kiterjedésű, konstans negatív görbületű Bolyai-Lobacsevkszki-felületen
élnek
formula szerint csökken. Tegyük fel az egyszerűség kedvéért, hogy
méterrúdjaik a hőmérséklettel arányosan változtatják hosszukat, tehát
a kör széléhez közelítve a méterrudak hossza nullához tart. Könnyen
belátható, hogy ha e körlap lakói úgy veszik, hogy méterrúdjaik hossza
mindenütt egyforma, akkor arra a konklúzióra jutnak, hogy egy végtelen
kiterjedésű, konstans negatív görbületű Bolyai-Lobacsevkszki-felületen
élnek
|
|
Mint ismeretes, az első nem euklideszi geometriák megalkotásakor Gauss
kísérletileg akarta eldönteni, hogy melyik a ,,helyes'' geometria.
Igaza volt-e Gaussnak? Részben igen, részben nem! Egyáltalán nem volt
igaza, ha azt akarta így eldönteni, hogy a nem euklideszi geometriák
helyesek-e, mint matematikai konstrukciók. Ez nem empirikus kérdés.
Kis leegyszerűsítéssel azt mondhatjuk, a matematikus olyan matematikai
struktúrát hoz létre, amilyet csak akar, feltéve, hogy a struktúrát
értelmező axiómarendszer ellentmondásmentes, s hogy a konstrukció
eleget tesz még néhány tradicionális elvárásnak. Ha ezeket valaki
geometriának nevezi, szíve joga, legfeljebb a publikálásnál fogják
tőle számon kérni, hogy milyen analógiák alapján nevezi így. Ha Gauss
a fényjelekből képzett háromszög szögeinek összegét azért kívánta
megmérni, mert ezzel arra keresett választ, hogy melyik geometria
írja le helyesen a fényjelek viselkedését, akkor igaza volt, hogy
ez egy empirikus kérdés. Tévedett viszont, ha arra gondolt, ezzel
majd eldönthető, hogy a lehetséges geometriák közül melyik a ,,világ
(pontosabban a fényjelek) geometriája'', hiszen önmagában a geometriát
az empirikus megfigyelésekből nem lehet kiolvasni, csupán a fizikai
elmélettel együtt vonatkoztatható az empirikus világra.
Összegezve tehát, matematikai értelemben sokféle geometria létezhet
és létezik. Abban a pillanatban azonban, amikor azt kérdezzük, ,,empirikus-e
a geometria'', vagyis eldönthető-e egy geometriai kérdés empirikusan,
a geometriára nem egyszerűen mint matematikai elméletre gondolunk,
hanem mint egy olyan elméletre, amely a világra vonatkozik. S mint
ilyent, máris a világról szóló (jelesül fizikai) elméletünk tartozékaként
kell felfognunk. Ennek megfelelően, csak e fizikai elmélettel együtt
vethető alá az empirikus konfirmációnak. Ebben a minőségében azonban,
mint Reichenbach helyesen hangsúlyozza,1 empirikusan szerzett tudásunk része.
Azt hihetnénk a fenti elemzések alapján, hogy a téridőnek csak a metrikus
tulajdonságai konvencionálisak, vagyis csak azok a tulajdonságok,
melyek meghatározzák az egyes események téridőbeli távolságát. S hogy
a topológiája a téridő struktúrájának olyan eleme, amely nem konvenció
jellegű. A következő példán keresztül szeretnék rámutatni, hogy ez
nem igaz. Misner és Wheeler mutatták meg először,2 hogy a vákuum Einstein-egyenleteknek létezik megoldása az
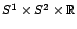 topológiában, vagyis egy olyan
téridő-sokaságon, melyben a térszerű hiperfelületek topológiája
topológiában, vagyis egy olyan
téridő-sokaságon, melyben a térszerű hiperfelületek topológiája
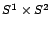 .
Ezeket a képződményeket nevezte Wheeler ,,féreglyukaknak''. A megoldás
érdekessége, hogy a féreglyuk két szája körül a téridő geometriája
olyan, mintha egy-egy külső Schwartzschild-megoldás lenne, vagyis
a vákuum egy ilyen topológiában úgy viselkedik, mintha ott nagy, pontszerű
tömegek lennének. Ezt a jelenséget nevezte Wheeler úgy, hogy
,,tömeg, tömeg nélkül''. Wheeler azt is megmutatta, hogy a csatolt
vákuum Einstein-Maxwell-egyenleteknek is létezik megoldása
a féreglyuk-topológiában. Ilyenkor a féreglyuk két szája nem csak
tömegként, hanem töltésként is viselkedik, miközben a tereknek
nincsenek a valóságban forrásaik, hiszen vákuummegoldásról van szó,
vagyis töltéseket látunk töltés nélkül (
.
Ezeket a képződményeket nevezte Wheeler ,,féreglyukaknak''. A megoldás
érdekessége, hogy a féreglyuk két szája körül a téridő geometriája
olyan, mintha egy-egy külső Schwartzschild-megoldás lenne, vagyis
a vákuum egy ilyen topológiában úgy viselkedik, mintha ott nagy, pontszerű
tömegek lennének. Ezt a jelenséget nevezte Wheeler úgy, hogy
,,tömeg, tömeg nélkül''. Wheeler azt is megmutatta, hogy a csatolt
vákuum Einstein-Maxwell-egyenleteknek is létezik megoldása
a féreglyuk-topológiában. Ilyenkor a féreglyuk két szája nem csak
tömegként, hanem töltésként is viselkedik, miközben a tereknek
nincsenek a valóságban forrásaik, hiszen vákuummegoldásról van szó,
vagyis töltéseket látunk töltés nélkül (![[*]](file:/usr/local/share/lib/latex2html/icons/crossref.gif) . ábra).
Wheeler példájával élve, ha egy fizikushallgatónak úgy alakítanánk
a tantervét, hogy először megtanítanánk neki a topológiát, utána megtanulná
a vákuum elektrodinamikát, vagyis a Maxwell-egyenleteket úgy, hogy
nem szerepelnek benne töltések és áramok, majd ezek után bevinnénk
egy laboratóriumba és demonstrálnák neki egy ponttöltés körüli elektromos
mező erővonalait, akkor ez a diák felkiáltana, ,,Jé, itt egy lyuk
van a térben, a tér nem egyszeresen összefüggő!''.
. ábra).
Wheeler példájával élve, ha egy fizikushallgatónak úgy alakítanánk
a tantervét, hogy először megtanítanánk neki a topológiát, utána megtanulná
a vákuum elektrodinamikát, vagyis a Maxwell-egyenleteket úgy, hogy
nem szerepelnek benne töltések és áramok, majd ezek után bevinnénk
egy laboratóriumba és demonstrálnák neki egy ponttöltés körüli elektromos
mező erővonalait, akkor ez a diák felkiáltana, ,,Jé, itt egy lyuk
van a térben, a tér nem egyszeresen összefüggő!''.
Figure:
,,Töltés, töltés nélkül''. Az Einstein-Maxwell-egyenletek
csatolt vákuum megoldása az
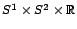 topológiában. A féreglyuk két szája körül az elektromos mező
olyan, mintha ott egy pozitív, illetve negatív töltés lenne, miközben
az elektromos mezőnek nincsenek forrásai, hiszen vákuummegoldásról
van szó
topológiában. A féreglyuk két szája körül az elektromos mező
olyan, mintha ott egy pozitív, illetve negatív töltés lenne, miközben
az elektromos mezőnek nincsenek forrásai, hiszen vákuummegoldásról
van szó
|
|
Megmutatható,3 hogy a tömeghez és az elektromos töltéshez hasonlóan létezik ,,Yang-Mills
töltés, Yang-Mills töltés nélül'', vagyis a többi részecskefizikai
kölcsönhatást leíró fizikai mezők töltései is generálhatók a tér nem
egyszeresen összefüggő topológiájával. Tehát a téridő topológiájában
is van egy konvencionális elem:
Vegyük észre azt a tudományfilozófiai szempontból figyelemreméltó
körülményt, hogy a téridő topológiájában és geometriájában fennálló
konvencionalitás egyben a fizikai elméletek konvencionalitását is
jelenti: a fizikai létezők olyan esszenciális attribútumainak,
mint a tömeg és a különböző töltések, már a puszta létezése
is csupán konvenció kérdése. Ezzel együtt, ismételten hangsúlyoznunk
kell, hogy a téridő struktúrájának elmélete és a fizikai elméletek,
együtt, már a valóság empirikusan tesztelhető tényeit írják le.
Poincaré konvencionalizmusa kapcsán heves vita bontakozott ki az irodalomban
arról, hogy vajon a tér dimenziója is egy konvenció csupán, mint ahogyan
ezt Poincaré szintén felveti, vagy természeti tény. Poincaré a következőt
írja:
A fizikai törvényeket differenciálegyenletekkel írjuk le, amelyekben
az anyagi pontok három koordinátája szerepel. Nem lehetne esetleg
ezeket a törvényeket más egyenletekkel kifejezni, ahol ez esetben
más, négy koordinátával jellemzett anyagi pontok jelennének meg?4
A dimenzió konvencionalitását nyilván úgy lehetne a legelegánsabban
bemutatni, ha felmutatnánk egy, a fenti példánkhoz hasonló olyan alternatív
,,
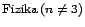 '' elméletet, melyre igaz
lenne, hogy
'' elméletet, melyre igaz
lenne, hogy
Logikailag nyilván megtehető például, hogy 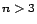 esetén a
esetén a
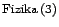 -hoz
hozzáveszünk olyan axiómákat, amelyek egyszerűen megszorítják az anyagi
pontok térkoordinátáit egy háromdimenziós altérre (részsokaságra).
Vagy például háromnál kisebb dimenzióban a fennmaradó térkoordinátákat
nem geometriai, hanem valamilyen fizikai változóknak tekintjük. Persze
ettől el lehet gondolni tetszetősebb megoldásokat is. Nem célunk itt,
hogy ilyeneket most kitaláljunk, csupán arra szeretnék rámutatni,
hogy azok a határozott érvek, melyeket Poincaréval szemben szoktak
megfogalmazni, tévesek. Egyik ilyen gyakran hangoztatott érv Ehrenfest-től
származik.5 Ehrenfest szerint, a tér háromdimenziós volta ,,empirikus, fizikai
tény''. A ponttöltés tere ugyanis
-hoz
hozzáveszünk olyan axiómákat, amelyek egyszerűen megszorítják az anyagi
pontok térkoordinátáit egy háromdimenziós altérre (részsokaságra).
Vagy például háromnál kisebb dimenzióban a fennmaradó térkoordinátákat
nem geometriai, hanem valamilyen fizikai változóknak tekintjük. Persze
ettől el lehet gondolni tetszetősebb megoldásokat is. Nem célunk itt,
hogy ilyeneket most kitaláljunk, csupán arra szeretnék rámutatni,
hogy azok a határozott érvek, melyeket Poincaréval szemben szoktak
megfogalmazni, tévesek. Egyik ilyen gyakran hangoztatott érv Ehrenfest-től
származik.5 Ehrenfest szerint, a tér háromdimenziós volta ,,empirikus, fizikai
tény''. A ponttöltés tere ugyanis
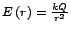 ,
tehát a távolság négyzetével csökken, ami csak háromdimenziós térben
igaz - hangzik az érv -, hiszen más dimenzióban a Poisson-egyenlet
megoldása nem
,
tehát a távolság négyzetével csökken, ami csak háromdimenziós térben
igaz - hangzik az érv -, hiszen más dimenzióban a Poisson-egyenlet
megoldása nem
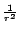 -es összefüggésre vezet. Ami a Poisson-egyenletet
illeti, ez igaz. Az érvelés azonban ott téved, amikor természetesnek
veszi, hogy egy tetszőleges
-es összefüggésre vezet. Ami a Poisson-egyenletet
illeti, ez igaz. Az érvelés azonban ott téved, amikor természetesnek
veszi, hogy egy tetszőleges 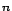 -dimenziós geometriát előfeltételezve,
az elektrosztatikai jelenségekre vonatkozó empirikus észleléseink
egy
-dimenziós geometriát előfeltételezve,
az elektrosztatikai jelenségekre vonatkozó empirikus észleléseink
egy 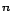 -dimenziós Poisson-egyenletre vezetnének. Ezt nemhogy nem
garantálja semmi, hanem - mint az Ehernfest által felmutatott problémákból
is kitűnik - egyenesen lehetetlen! A
-dimenziós Poisson-egyenletre vezetnének. Ezt nemhogy nem
garantálja semmi, hanem - mint az Ehernfest által felmutatott problémákból
is kitűnik - egyenesen lehetetlen! A
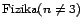 nem
egyszerűen abból áll, hogy a
nem
egyszerűen abból áll, hogy a
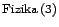 minden
formulájában, ahol a dimenzió megjelenik, a hármast kicseréljük
minden
formulájában, ahol a dimenzió megjelenik, a hármast kicseréljük 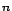 -re.
Például a Maxwell-egyenletek, melyekbol az elektrosztatika Poisson-egyenletét
származtatjuk, nem háromdimenziós térben fel sem írhatók a szokásos
alakjukban, hiszen a rotációnak csak három dimenzióban van értelme
(legalábbis csak ott lesz egy vektor). Hasonlóképpen a vektoriális
szorzatnak sincs értelme, csak három dimenzióban. Vagyis a fizika
törvényei egy más dimenzióban nem a háromdimenziós fizikai törvények
,,kézenfekvő matematikai általánosítása'' útján tárhatók fel, hanem
úgy, hogy a legelemibb empirikus tapasztalatainktól elindulva, egy
nem háromdimenziós geometria nyelvén mindent újrafogalmazunk, és egy
új fizikát építünk fel. Ember legyen a talpán, aki előre megmondja,
hogy mi lenne egy ilyen programnak a végeredménye! Nem látunk példát
ennek a programnak még csak a részleges megvalósítására sem,6 hiszen nincs semmilyen praktikus motivációja annak, hogy ezt megtegyük.
Itt most csupán az a fontos, hogy Poincarénak az a felvetése, hogy
esetleg a dimenzió is csupán konvenció kérdése, nem alaptalan, és
hogy az ellenkezőjére nincs semmilyen empirikus, fizikai bizonyíték.
-re.
Például a Maxwell-egyenletek, melyekbol az elektrosztatika Poisson-egyenletét
származtatjuk, nem háromdimenziós térben fel sem írhatók a szokásos
alakjukban, hiszen a rotációnak csak három dimenzióban van értelme
(legalábbis csak ott lesz egy vektor). Hasonlóképpen a vektoriális
szorzatnak sincs értelme, csak három dimenzióban. Vagyis a fizika
törvényei egy más dimenzióban nem a háromdimenziós fizikai törvények
,,kézenfekvő matematikai általánosítása'' útján tárhatók fel, hanem
úgy, hogy a legelemibb empirikus tapasztalatainktól elindulva, egy
nem háromdimenziós geometria nyelvén mindent újrafogalmazunk, és egy
új fizikát építünk fel. Ember legyen a talpán, aki előre megmondja,
hogy mi lenne egy ilyen programnak a végeredménye! Nem látunk példát
ennek a programnak még csak a részleges megvalósítására sem,6 hiszen nincs semmilyen praktikus motivációja annak, hogy ezt megtegyük.
Itt most csupán az a fontos, hogy Poincarénak az a felvetése, hogy
esetleg a dimenzió is csupán konvenció kérdése, nem alaptalan, és
hogy az ellenkezőjére nincs semmilyen empirikus, fizikai bizonyíték.
Egyes feltételezések szerint (pl. Einstein), ugyanez a helyzet a Lorentz-elméletre
és a relativitáselméletre nézve:
Einstein jól ismerte, tisztelte, s bizonyos értelemben el is fogadta
Poincaré konvencionalista álláspontját,
egy kalap alá véve Kanttal, mondván, hogy ,,Az empirikus adatok értelmezéséhez
gondolkodásra van szükség. A fogalmak és kategóriák elkerülhetetlenek,
hiszen a goldolkodás elválaszhatatlan elemei.''7 Ha Kant megelégedett volna ezzel a megállapítással - írja -,
akkor elkerülhette volna a szkepticizmust. ,,Valójában azonban Kant
annak a tévedésnek esett áldozatául (s ezt nehéz lett volna az ő idejében
elkerülnie), hogy az euklideszi geometria a gondolkodásunk számára
szükségszerűen adott, és hiteles (azaz az érzéki tapasztalástól független)
tudást nyújt a megértendő »külső« világra vonatkozóan.''8 Einstein világosan látta, hogy Kantnak ettől a tévedésétől egyenes
út vezetett az a priori szintetikus ítéletekig.
Einstein a téridő geometriáját a világról való fogalmi
gondolkodás kiinduló lépésének tekintette, egy olyan választásnak,
amelyet nem lehet, és - szerinte - nem is szükséges empirikusan
alátámasztani. ,,Valójában egyetlen fizikai elmélet sem teljesíti
ezt a követelményt'' - írja Percy Bridgmannal
polemizálva. ,,Hogy egy elmélet fizikai elméletnek legyen tekinthető,
csupán az szükséges, hogy a belőle levezethető állítások, elvben,
empirikusan ellenőrizhetők legyenek.''9
A DQ tézist vagy más néven aluldeterminációs tézist sokféle, különböző
erősségű formában szokás érteni. Kezdjük a leggyengébb verzióval:
- U1
- Elvben nem zárható ki, hogy empirikus adatok egy halmazát több
különböző elmélet is képes leírni. (Hume)
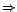 Következésképpen minden ,,empirikus evidencia'' relatív
egy elméletre nézve, abban az értelemben, hogy az elmélet határozza
meg, hogy minek az evidenciája.
Következésképpen minden ,,empirikus evidencia'' relatív
egy elméletre nézve, abban az értelemben, hogy az elmélet határozza
meg, hogy minek az evidenciája.
- U2
- Nem lehetséges sem megerősíteni sem cáfolni egy elmélet kiragadott
részét, csak az egész elméletet. (Quine-holizmus, Quine Carnap-kritikája))
- U3
- Egy
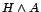
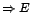 szerkezetű elmélet esetén az
szerkezetű elmélet esetén az
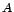 feltevésrendszer mindig módosítható úgy, hogy
feltevésrendszer mindig módosítható úgy, hogy 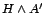
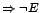 .
(Duhem)
.
(Duhem)
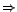 Következésképpen nem lehetséges egy
Következésképpen nem lehetséges egy 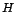 hipotézist
valamely empirikusan tesztelhető -
hipotézist
valamely empirikusan tesztelhető - 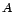 feltétel melletti - következményének
nemteljesülésével megcáfolni.
feltétel melletti - következményének
nemteljesülésével megcáfolni.
- U4
- Tetszőleges elmélet racionálisan megtartható, függetlenül attól,
hogy milyen empirikus evidenciákkal bírunk. (Quine: Két dogma)
Laudan (A ,,Demistifying''-ban) ide sorolja az induktív általánosítás
és az tudományos extrapoláció aluldetermináltságát (ampliatív aluldetermináció)
is. Mivel ez más természetű aluldetermináltság, ezt az indukció problémájának
tárgyalásánál fogjuk megvizsgálni.
- U1 és U2 nyilvánvalóan igaz. A Poincaré-féle konvencionalizmus példa
ezekre. Mint Grünbaum helyesen mutat rá10, a Poincaré-féle tézis azonban nem támasztja alá U3-at és U4-et.
- U3 és U4 messze nem triviális, hogy igaz lenne, és DQ egyáltalán nem
bizonyította be, hogy így van. A probléma a következő. Éppen a holizmusból
következően, ha egy
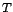 elmélet egésze ellentmond egy evidenciának,
akkor az elméletet falszifikáltuk, mint egészet. Tegyük fel, találtunk
egy új
elmélet egésze ellentmond egy evidenciának,
akkor az elméletet falszifikáltuk, mint egészet. Tegyük fel, találtunk
egy új 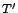 elméletet, amely kompatibilis az összes evidenciával.
De mi garantálná, hogy azt, hogy
elméletet, amely kompatibilis az összes evidenciával.
De mi garantálná, hogy azt, hogy 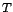 és
és 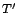 olyan szerkezetűek,
hogy
olyan szerkezetűek,
hogy 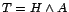 illetve
illetve 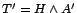 ? Még kevésbé igaz ez
a
? Még kevésbé igaz ez
a 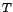 elmélet tetszőleges
elmélet tetszőleges 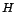 részére.
részére.
- Ha csak U1 és U2 tartható, abból nem következik, hogy ,,anything
goes''.
- Laudan jogosan bírálja azokat, akik U1 és U2 tézisekből kiindulva
az ,,episztemológiát szociologizálják'' (történetesen Hesse-vel
és Bloorral polemizál). Bírálata azonban célt téveszt. Mert a szociológiai
program helyesen gondolja, hogy az elméletek empirikus aluldetermináltsága
megnyitja az utat azokhoz a vizsgálatokhoz, hogy a ténylegesen felmerült,
egymással rivalizáló elméletek közötti választásnak milyen nem-deduktív
és nem empirikus elemei lehetnek. A tévedés ott történik, amikor az
elméletválasztásnak ezt a problémáját episztemológiai kérdésnek tekintik.11
A relativitáselméletről mondottakból világosan kiderült, hogy a relativitáselmélet
és a klasszikus fizika (Lorentz-elmélet) viszonya nem illik bele a
Poincaré-féle konvencionalista sémába. A tévedés gyökere, az a feltételezés,
mely szerint a Lorentz-elméletben extra feltevéseket teszünk (kell
tennünk) a méterrudak és órák deformációjára, a MM interferométer
karjainak kontrakciójára, stb. nézve, ahhoz, hogy az empíriával egyező
eredményeket kapjunk, míg a relativitáselméletben nem. Jól jellemzi
ezt pl. Lánczos Kornél következő mondata:
A [Michelson-Morley] kísérlet negatív eredménye arra késztette
Lorentzet, hogy feltételezze [kiemelés tőlem - Sz. L.]:
az éterhez viszonyított mozgás hatására a mozgás irányába eső távolságok
megrövidülnek (ez a Fitzgerald-Lorentz-féle kontrakciós hipotézis),
és így kompenzálja azt a jelenséget, amely minden más esetben fellépne.12
Vagyis, mintha az lenne a helyzet, hogy
De a relativisztikus fizika ugyanúgy tartalmazza a fizikai deformációkat,
tehát a helyzet a következő:
és persze ez csak úgy és azért lehetséges mert
csak az egyik 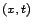 a másik
a másik 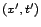 változókban kifejezve. Tehát
- mint korábban kifejtettük - a két elmélet minden vonatkozásban
ugyanaz. Az egyetlen különség a ,,tér'' és ,,idő'' szavak
használatában van.
változókban kifejezve. Tehát
- mint korábban kifejtettük - a két elmélet minden vonatkozásban
ugyanaz. Az egyetlen különség a ,,tér'' és ,,idő'' szavak
használatában van.
E megállapításunk rávilágít arra, hogy Poincaré konvencionalista felfogását
is újra átgondoljuk. Abban a szabadságban, hogy a téridő geometriáját
megválaszthatjuk, a konvencionalitásnak két esete keveredik egyszerre:
- Nem triviális konvencionalizmus:
az elméletek empirikusan aluldetermináltak.
- Szemantikai konvencionalizmus: az elnevezés szabadsága, vagyis
az a szabadságunk, hogy az empirikusan értelmezett (fizikai) mennyiségek
közül mit minek nevezünk, például melyiket nevezzük tér- illetve időkoordinátának.
Az empirikus aluldetermináltságra példa a téridő topológiájának konvencionális
jellege. Ebben az esetben tisztán látjuk érvényesülni a Poincaré által
tételezett választás szabadságát a téridő lehetséges struktúrái és
a hozzájuk tartozó fizikai elméletek között. Ez egyben példa az empíria
,,elmélet-terhességére'' is. Gondoljunk Wheeler fizikushallgatójára:
a laboratóriumban látott egyszerű jelenség a tér nem triviális topológiájának
éppúgy lehet az evidenciája, mint a töltés létezésének, s ez csupán
az elméleti előfeltevésektől függ.
Ugyanakkor Poincaré korongos példájában szó sincs az empíriát megelőző
elméleti feltevésekről, és arról a fajta konvencionalitásról, melynek
illusztrálására a példa született. Egyszerű szemantikai konvencióról
van szó! Túl könnyen, és túl gyakran szokás az empíriát megelőző
elméleti feltevésekről beszélni! Olyan egyszerű mérési operáció,
mint a távolság mérése - állítja Reichenbach13 - nem végezhető el, pontosabban nem értelmezhető anélkül az elméleti
előfeltevés nélkül, hogy a merev méterrúd egy szakasz mentén egymás
után lehelyezve nem változtatja a hosszát, pontosabban, hogy nincsen
olyan univerzális deformáció, melyet a méterrudak is és azok az objektumok
is, melyek hosszát mérni kívánjuk, elszenvednek. A koronglakók példájára
lefordítva, a távolságmérés során más eredményre ,,jutnak'', és ezzel
a világuk geometriáját másnak fogják ,,tapasztalni'', ha azzal az
elméleti előfeltevéssel élnek, hogy a világuk hőmérséklete állandó,
illetve, ha változik - állítja Poincaré. Jobban meggondolva azonban
- hasonlóan a relativitáselmélet kontra Lorentz-elmélet esetéhez
-, ez nem igaz! Egyszerűen kétféle fizikai mennyiséget vezethetünk
be:
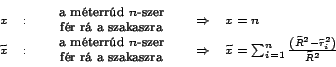
ahol
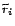 az
az 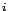 -edik helyen álló méterrúd
-edik helyen álló méterrúd 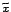 -távolsága
a középponttól, azaz a második esetben minden egyes ,,métert'' egy
-távolsága
a középponttól, azaz a második esetben minden egyes ,,métert'' egy
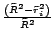 faktorral súlyozunk. Ebből a szempontból mindegy, hogy milyen teoretikus
előfeltevések alapján definiáljuk így az egyik mennyiséget illetve
a másikat, a lényeg az, hogy empirikus értelemben két különböző mennyiséget
értelmeztünk. Hasonlóan két további fizikai mennyiséget értelmezhetünk:
faktorral súlyozunk. Ebből a szempontból mindegy, hogy milyen teoretikus
előfeltevések alapján definiáljuk így az egyik mennyiséget illetve
a másikat, a lényeg az, hogy empirikus értelemben két különböző mennyiséget
értelmeztünk. Hasonlóan két további fizikai mennyiséget értelmezhetünk:
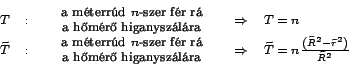
Most, hogy 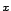 vagy
vagy 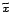 mennyiséget nevezzük
,,távolságnak'', nem igazán jelentős kérdés, illetve az sem különösebben
fontos, hogy
mennyiséget nevezzük
,,távolságnak'', nem igazán jelentős kérdés, illetve az sem különösebben
fontos, hogy 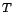 -t vagy
-t vagy 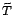 -ot kereszteljük el ,,hőmérsékletnek''.
Ez az a szabadság, melyet szemantikai konvencionalizmusnak nevezünk.
Bárhogyan is döntöttünk az elnevezések ügyében, a fizika törvényeit
és a tér geometriáját a valóság, a mérési eredmények egyértelműen
meghatározzák: Fizikai törvény lesz például, hogy
-ot kereszteljük el ,,hőmérsékletnek''.
Ez az a szabadság, melyet szemantikai konvencionalizmusnak nevezünk.
Bárhogyan is döntöttünk az elnevezések ügyében, a fizika törvényeit
és a tér geometriáját a valóság, a mérési eredmények egyértelműen
meghatározzák: Fizikai törvény lesz például, hogy
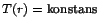 ,
illetve az is, hogy
,
illetve az is, hogy
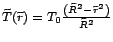 .
Hasonlóan, a mérési eredmények egyértelműen determinálják, hogy az
.
Hasonlóan, a mérési eredmények egyértelműen determinálják, hogy az
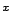 -geometria nem euklideszi, az
-geometria nem euklideszi, az 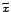 -geometria pedig
euklideszi. Miután tehát eldöntöttük, hogy mit jelent a ,,távolság''
szó, az
-geometria pedig
euklideszi. Miután tehát eldöntöttük, hogy mit jelent a ,,távolság''
szó, az 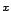 , vagy az
, vagy az 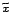 mennyiséget, a mérések egyértelműen
meghatározzák a tér geometriáját. Hasonlóan az, hogy a hőmérséklet
a mérések szerint állandó, vagy változik, csupán attól függ, hogy
az állandó
mennyiséget, a mérések egyértelműen
meghatározzák a tér geometriáját. Hasonlóan az, hogy a hőmérséklet
a mérések szerint állandó, vagy változik, csupán attól függ, hogy
az állandó 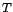 , vagy a radiálisan csökkenő
, vagy a radiálisan csökkenő 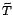 mennyiséget
kereszteljük el ,,hőmérsékletnek''. Nincs tehát szó két fizikai elméletről
és két térgeometriáról, csupán a szavak más használatáról!
mennyiséget
kereszteljük el ,,hőmérsékletnek''. Nincs tehát szó két fizikai elméletről
és két térgeometriáról, csupán a szavak más használatáról!
Laszlo E. Szabo
2003-03-27
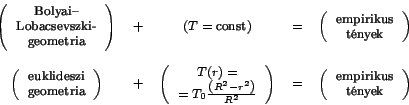
![\includegraphics[%
scale=0.5]{korong.eps}](img5.gif)
![]() topológiában, vagyis egy olyan
téridő-sokaságon, melyben a térszerű hiperfelületek topológiája
topológiában, vagyis egy olyan
téridő-sokaságon, melyben a térszerű hiperfelületek topológiája
![]() .
Ezeket a képződményeket nevezte Wheeler ,,féreglyukaknak''. A megoldás
érdekessége, hogy a féreglyuk két szája körül a téridő geometriája
olyan, mintha egy-egy külső Schwartzschild-megoldás lenne, vagyis
a vákuum egy ilyen topológiában úgy viselkedik, mintha ott nagy, pontszerű
tömegek lennének. Ezt a jelenséget nevezte Wheeler úgy, hogy
,,tömeg, tömeg nélkül''. Wheeler azt is megmutatta, hogy a csatolt
vákuum Einstein-Maxwell-egyenleteknek is létezik megoldása
a féreglyuk-topológiában. Ilyenkor a féreglyuk két szája nem csak
tömegként, hanem töltésként is viselkedik, miközben a tereknek
nincsenek a valóságban forrásaik, hiszen vákuummegoldásról van szó,
vagyis töltéseket látunk töltés nélkül (
.
Ezeket a képződményeket nevezte Wheeler ,,féreglyukaknak''. A megoldás
érdekessége, hogy a féreglyuk két szája körül a téridő geometriája
olyan, mintha egy-egy külső Schwartzschild-megoldás lenne, vagyis
a vákuum egy ilyen topológiában úgy viselkedik, mintha ott nagy, pontszerű
tömegek lennének. Ezt a jelenséget nevezte Wheeler úgy, hogy
,,tömeg, tömeg nélkül''. Wheeler azt is megmutatta, hogy a csatolt
vákuum Einstein-Maxwell-egyenleteknek is létezik megoldása
a féreglyuk-topológiában. Ilyenkor a féreglyuk két szája nem csak
tömegként, hanem töltésként is viselkedik, miközben a tereknek
nincsenek a valóságban forrásaik, hiszen vákuummegoldásról van szó,
vagyis töltéseket látunk töltés nélkül (![]() . ábra).
Wheeler példájával élve, ha egy fizikushallgatónak úgy alakítanánk
a tantervét, hogy először megtanítanánk neki a topológiát, utána megtanulná
a vákuum elektrodinamikát, vagyis a Maxwell-egyenleteket úgy, hogy
nem szerepelnek benne töltések és áramok, majd ezek után bevinnénk
egy laboratóriumba és demonstrálnák neki egy ponttöltés körüli elektromos
mező erővonalait, akkor ez a diák felkiáltana, ,,Jé, itt egy lyuk
van a térben, a tér nem egyszeresen összefüggő!''.
. ábra).
Wheeler példájával élve, ha egy fizikushallgatónak úgy alakítanánk
a tantervét, hogy először megtanítanánk neki a topológiát, utána megtanulná
a vákuum elektrodinamikát, vagyis a Maxwell-egyenleteket úgy, hogy
nem szerepelnek benne töltések és áramok, majd ezek után bevinnénk
egy laboratóriumba és demonstrálnák neki egy ponttöltés körüli elektromos
mező erővonalait, akkor ez a diák felkiáltana, ,,Jé, itt egy lyuk
van a térben, a tér nem egyszeresen összefüggő!''.
![\includegraphics[%
width=0.80\columnwidth]{fereglyuk.ps}](img10.gif)